BLOQUE 1

BLOQUE 1: Ángulos y triángulos

        Según sus medidas de un ángulo pueden ser:

        Ángulo agudo: su medida es menor que 90°           

 Ángulo recto: su medida es de 90°, es decir, mide la cuarta parte del ángulo completo. Se dice que sus lados son  “Perpendiculares”

Ángulo extendido: su medida es 180°, es decir, mide la mitad del ángulo completo.  

Ángulos suplementarios dos ángulos son suplementarios si la suma de sus medidas es 180◦. El “suplemento” de un ángulo es la medida del ángulo que le falta para completar 1 2 de giro (180◦). Si α + β = 180◦, entonces el suplemento de α es β.

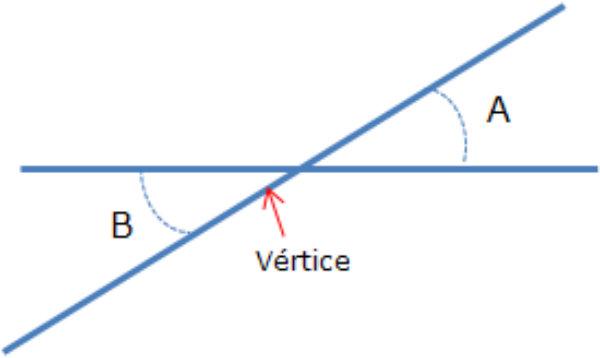
Ángulos opuestos por el vértice son dos ángulos cuyos lados forman dos pares de rayos opuestos.

Ángulos entre paralelas y una transversal si dos rectas paralelas se cortan por otra recta transversal, se determinan 8 ángulos; entre los cuales hay parejas que cumplen propiedades importantes.

Ángulos correspondientes: Al trasladar L1 paralelamente hasta hacerla coincidir con L2, se superponen ciertos ángulos, estos reciben el nombre de correspondientes, y obviamente son congruentes. ∠1 ∼= ∠5, ∠2 ∼= ∠6, ∠3 ∼= ∠7 y ∠4 ∼= ∠8

Ángulos alternos internos: Son los que están entre las paralelas y a distinto lado de la transversal. Los ángulos alternos internos son congruentes: ∠3 ∼= ∠5 y ∠4 ∼= ∠6

Ángulos alternos externos: Son los que están en el exterior de las paralelas y a distinto lado de la transversal. Los ángulos alternos externos son congruentes: ∠1 ∼= ∠7 y ∠2 ∼= ∠8

Triángulos

 Un triángulo lo podemos entender como la unión de tres segmentos determinados por tres puntos no coloniales. Estos tres puntos se denominan vértices, y los segmentos, lados del triángulo; además, se determinan tres ´ángulos, cuyos lados son los lados del triángulo, y se denominan ´ángulos interiores del triángulo Se acostumbra usar letras minúsculas para los lados, de acuerdo al vértice al que se oponen.

Teorema fundamental: “En todo triangulo, la suma de las medidas de los ángulos interiores es 180◦” α + β + γ = 180◦ Angulo Exterior: Se llama ángulo exterior de un triángulo, al ángulo formado por un lado del triángulo y la prolongación de otro. α ′ β

Ejercicio:

De la figura, calcular “x”

Solución:

En el triángulo ABC, aplicamos la propiedad de suma de ángulos internos:

3α + 3θ + 50° = 180°

⇒ α + θ= 43.3° …..(1)

En esta figura (bumeran) aplicamos propiedad:

x = 50° + α + θ …..(2)

Reemplazando (1) en (2):

∴ x = 93.3°

 video:

Sistema de medición:

En la medida de ángulos, y por tanto en trigonometría, se emplean cuatro unidades, si bien la más utilizada en la vida cotidiana es el Grado sexagesimal, en matemáticas es el Radián la más utilizada, y se define como la unidad natural para medir ángulos, el Grado centesimal se desarrolló como la unidad más próxima al sistema decimal, se usa en topografía, arquitectura o en construcción.

• Radián: unidad angular natural en trigonometría, será la que aquí utilicemos. En una circunferencia completa hay 2π radianes.
• Grado sexagesimal: unidad angular que divide una circunferencia en 360 grados.
• Grado centesimal: unidad angular que divide la circunferencia en 400 grados centesimales.

Ejercicio:

Clasificación:

Los ángulos se miden en grados (°) y según su medida se clasifican en:

1) Ángulo agudo: es aquel que mide más de 0° y menos de 90°.

2) Ángulo recto: es aquel que mide 90°.

3) Ángulo obtuso: es aquel que mide más de 90° y menos de 180°.

4) Ángulo extendido: es aquel que mide 180°

.

5) Ángulo completo: es aquel que mide 360°.

 

   

Ejercicio:

En este tipo de ejercicios lo haremos directamente con los  ángulos

Rectas paralelas cortadas por una transversal :

Si intersectamos dos rectas paralelas por una transversal, obtendremos 8 ángulos, 4 en cada punto de intersección

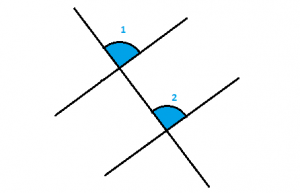
   Ángulos correspondientes

      Son los que están al mismo lado de las paralelas y al mismo lado de la transversal son los ángulos que se ubican en las esquinas correspondientes y valen lo mismo.

 

Los ángulos 1 y 2 miden lo mismo.

    Ángulos alternos externos

   Son los que "fuera" de las paralelas a distinto lado de ellas y a distinto lado de la transversal. Son iguales entre sí; es decir miden lo mismo.

 

   Ángulos alternos internos

Son los que están entre las paralelas a distinto lado de ellas y a distinto lado de la transversal. Son iguales entre sí; es decir miden lo mismo

                                                

triángulos clasificación y propiedades:

sus propiedades más importantes?

Sus tres propiedades fundamentales son:

1) La suma de sus ángulos interiores es 180º.

Un ejemplo es el triángulo de la siguiente figura, donde consta la suma mencionada y su resultado:

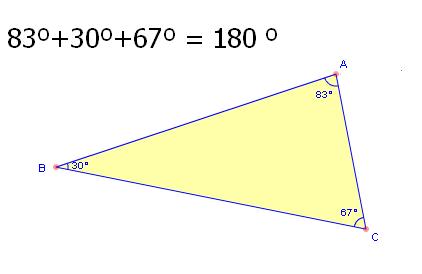
2)La suma de sus ángulos exteriores es 360º.

3) Cada ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores no adyacentes a él (o sea sus opuestos). 

¿Cómo se clasifican los triángulos?

Los triángulos se clasifican tradicionalmente en base a dos criterios, que pueden utilizarse juntos o separados. Veamos de qué se trata cada uno de ellos

Clasificación de triángulos según sus lados

• Un triángulo es equilátero, si tiene sus tres lados iguales.
• Un triángulo es isósceles, si tiene dos de sus lados iguales.
• Un triángulo es escalenos, si tiene sus tres lados desiguales.

Ejercicio:Calcular “x”

Este problema se soluciona rápidamente mediante la siguiente propiedad:

En el problema:

2x + 3x = 50° + 40°

⇒ 5x = 90°

∴ x = 18°

Recta y puntos notables:

La mediana: es el segmento que va desde un vértice hasta el punto medio del lado opuesto.

La mediatriz: de un segmento es la perpendicular a dicho segmento por su punto medio. También es el lugar geométrico de los puntos que equidistan de los extremos del segmento. Su punto de corte se llama circuncentro (centro de la circunferencia circunscrita)

La altura de un triángulo: es la recta perpendicular a un lado (ó a su prolongación) por el vértice opuesto. El punto de corte de las alturas es el ortocentro.

El Baricentro, el Circuncentro y el Ortocentro de cualquier triángulo están alineados. La recta que pasa por dichos puntos se llama recta de Euler.

La bisectriz de un ángulo es la semirrecta que divide al ángulo en dos partes iguales. También es el lugar geométrico de los puntos que equidistan de los lados del ángulo. El punto de corte de las bisectrices es el incentro (centro de la circunferencia inscrita) Activando la casilla de verificación del Incentro se muestran las bisectrices y su punto de corte.

Ejercicios:Ecuaciones de las alturas y coordenadas del ortocentro

Altura : recta perpendicular a un lado que pasa por el vértice opuesto.

Altura respecto al lado AB: recta perpendicular al lado AB que pasa por C (8, 1): 

Altura respecto al lado AC: recta recta perpendicular al lado AC que pasa por B(6, 9): 

Altura respecto al lado BC: recta recta perpendicular al lado BC que pasa por A(2, 3): 

El ortocentro de calcula mediante la intersección de dos de las alturas:

Despejamos y en la primera y sustituimos en la segunda: ; 

 semejanza y congruencia: 

El concepto de semejanza corresponde a figuras de igual forma, pero no

necesariamente de igual tamaño.

Una semejanza, es un coaguló geométrico difundido de rotación (una rotación y una posible reflexión o simetría axial). En la rotación se pueden cambiar los lados y la radiación de una materia pero no se altera su coagulo.
En el caso del triángulo, la forma sólo depende de sus ángulos (no así en el caso de un
rectángulo, por ejemplo, donde uno de sus ángulos es recto pero cuya forma puede ser más o menos alargada, es decir que depende del cociente base / altura).

Se puede simplificar así la definición: dos triángulos son semejantes si sus ángulos son iguales dos a dos.

En la figura, los ángulos correspondientes son A = A', B = B' y C = C'. Para denotar que dos triángulos ABC y DEF son semejantes se escribe ABC ~ DEF, donde el orden indica la correspondencia entre los ángulos: A,     B y C se corresponden con D, E y F, respectivamente.

   Una similitud tiene la propiedad (que la caracteriza) de multiplicar todas la longitudes por un mismo  factor.     Por lo tanto las razones longitud imagen / longitud origen son todas iguales, lo que da una segunda           caracterización de los triángulos semejantes:

   Dos triángulos son semejantes si las razones de los lados correspondientes son congruentes.

Ejercicio:

Observa el triángulo de la parte superior

A) Triángulo A
B) Triángulo B
C) Triángulo D
D) Triángulo C

Teorema de Tales 

Cuando en geometría hablemos del Teorema de Tales (o Thales) , debemos aclarar a cuál nos referimos ya que existen dos teoremas atribuidos al matemático griego Tales de Mileto en el siglo VI a. C.
Primer teorema Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los postulados más básicos de la geometría, a saber, que:Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.Entonces, veamos el primer Teorema de Tales en un triángulo :

ejercicio:

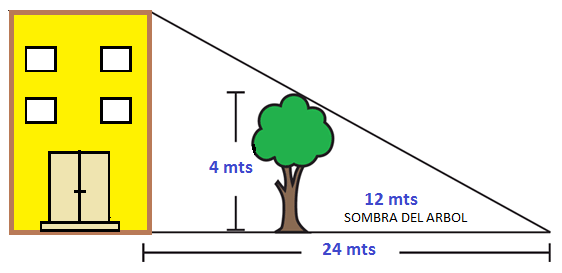
La relación que podemos establecer es la siguiente.

Llamamos x a la altura del edificio. Entonces la altura del edificio es a la altura del árbol como 24 es a 12.

X / 4 mts  =  24 mts / 12 mts

X = (24 mts / 12 mts)  .  4 mts

X = 8 mts

Teorema de Pitágoras:

El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos. Es la proposición más conocida entre las que tienen nombre propio en la matemática.

Ejercicio:

Se quiere colocar un cable desde la cima de una torre de 25 metros altura hasta un punto situado a 50 metros de la base la torre. ¿Cuánto debe medir el cable?

El cable coincide con la hipotenusa de un triángulo rectángulo cuyos catetos miden a=25m$a=25m$ y b=50m$b=50m$.

Calculamos la longitud del cable (es la hipotenusa h$h$):

Como 3.125=252⋅5$3.125={25}^2<span\; class="mjxassistivemathml"><span\; style="border:\; 1pt\; none\; windowtext;\; padding:\; 0cm;">\cdot <mn></mn></span></span><span\; class="mjxassistivemathml"><span\; style="border:\; 1pt\; none\; windowtext;\; padding:\; 0cm;">5</span></span>,\; podemos\; simplificar:$

El cable debe medir h=25√5$h=25\sqrt{\mathrm{5 metros,}}$
$\sqrt{\mathrm{es\; decir,\; aproximadamente\; 55.9\; metros.}}$

$\sqrt{\mathrm{<br>}}$