Propiedades de los polígonos
Un polígono con n lados, tienen como suma de sus ángulos interiores 180° (n -2)
Se toma como referencia un vértice cualquiera y se trazan (n – 2) triángulos en el polígono.
la suma de los ángulos de un triángulos es 180°.
Es fácil ver que la suma de los ángulos interiores del polígono, es la suma de los ángulos de los triángulos.
A + B + C + D + E = 190° (n – 2)
Si el polígono es regular, y se desea calcular el valor del angulo interior basta con dividir 180° (n – 2) entre el numero de lados del polígono.
La suma de los ángulos exteriores de un polígono es igual a 360°
La suma de los ángulos interiores y exterior de un vértice del polígono es de 180°.
La suma de los ángulos interiores y exteriores del polígonos es 180° n.
Por lo tanto, a 180° n restamos la suma de los ángulos interiores 180° (n – 2).
180° n – 180° (n – n + 2) = 360°
Suma de ángulos exteriores = 360°
3. El total de diagonales que se pueden trazar en un polígono de n lados, se obtiene con la expresión:
Video:
Polígonos ELEMENTOS Y CLASIFICACIÓN
Elementos
Estos son los elementos de un polígono:
· Lado: uno de los segmentos antes nombrados que delimita la superficie del polígono.
· Vértice: punto donde se unen dos segmentos de los que conforman el polígono.
· Diagonal: segmento que une dos vértices no adyacentes.
· Ángulo: apertura de los dos segmentos adyacentes que concurren en un vértice.
Para poder identificar fácilmente los elementos de un polígono existe una notación muy sencilla que nos facilita saber de que elemento estamos hablando en cada momento. Así podremos diferenciar los lados, vértices o cualquier otro elemento entre si.
Ejemplo:
Clasificación
Veamos ahora la clasificación de los polígonos regulares según su número de lados:
Nombre
|
Número de lados
|
No existe
|
1
|
No existe
|
2
|
Triángulo
|
3
|
Cuadrado
|
4
|
Pentágono
|
5
|
Hexágono
|
6
|
Heptágono
|
7
|
Octógono
|
8
|
Eneágono
|
9
|
Decágono
|
10
|
ANGULO CENTRAL:
son los que se forman con vértice en el centro del polígono, y cuyos lados son los radios que unen ese centro a dos vértices consecutivos. Por lo tanto, un polígono regular tiene tantos ángulos centrales, todos iguales, como lados. Por lo tanto, como la medida de la suma de todos los ángulos que pueden formarse alrededor de un punto, es de 360° la medida del ángulo central de un polígono regular es igual a 360 dividido por la cantidad de lados.

· Ángulo central del triángulo equilátero: 360° ÷ 3 = 120°.
· Ángulo central del cuadrado: 360° ÷ 4 = 90°.
· Ángulo central del pentágono: 360° ÷ 5 = 72°.
· Ángulo central del hexágono: 360° ÷ 6 = 60°.
· Ángulo central del octágono: 360° ÷ 8 = 45°.
· Ángulo central del decágono: 360° ÷ 10 = 36°.
Ejemplo:
Si n es el número de lados de un polígono:

Ángulo central = 360° : n
Ángulo central del pentágono regular= 360° : 5 = 72º
ANGULO INTERIOR:
En geometría, un ángulo interior o ángulo interno es un ángulo formado por dos ladosde un polígono que comparten un vérticecomún, está contenido dentro del polígono. Un polígono simple tiene sólo un ángulo interno por cada vértice.
En el plano euclídeo, si todos los ángulos interiores de un polígono no superan los 180 grados sexagesimales o radianes, se clasifican como polígonos convexos. Si existe por lo menos un ángulo interior superior
a 180 grados o radianes, se trata de un polígono cóncavo.
Si todos los ángulos interiores de un polígono simple y convexo son iguales y todos sus lados tienen la misma longitud, se trata de un polígono regular. En caso contrario, se trata de un polígono irregular.

Ejercicio:
calcula la medida del angulo interior de un hexágono
solución:
n=5 i=(n-2)180°
----------------
n
=(6-2)180°
------------------
6
=4(180°)
----------------
6
= 720°
-------------
6
= 120°
ANGULO EXTERIOR
En general, un ángulo externo, exterior o ángulo exterior a un polígono, es aquel que está entre un lado de un polígono y la línea que se extiende desde el lado adyacente. Éste y el ángulo exterior en el mismo vértice son suplementarios, es decir, suman 180⁰.
Un ángulo externo es aquel que es formado por un lado de un polígono y la prolongación del lado adyacente. Éste se encuentra en la parte exterior del polígono.
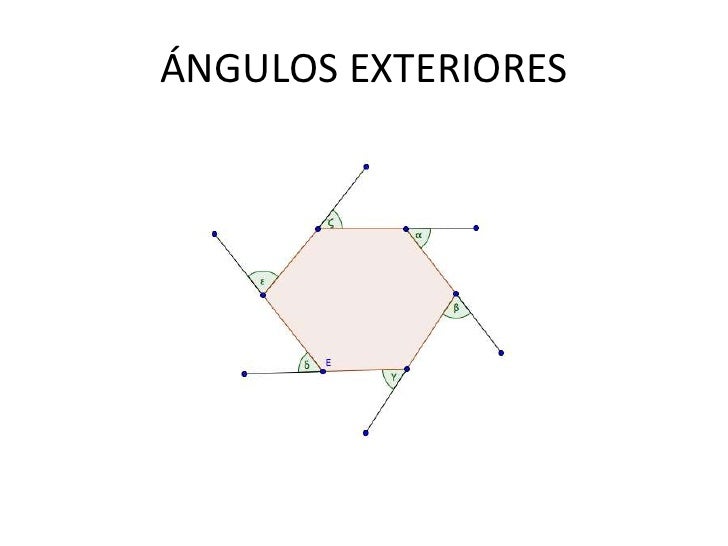
SUMA DE ANGULOS INTERIORES Y EXTERIORES:
En un triángulo existen dos tipos de ángulos: los ángulos interiores lo forman dos lados y los ángulos exteriores lo forman un lado y su prolongación.
Sus propiedades son:
La suma de los ángulos interiores de un triángulo es igual a 180°.
A + B + C = 180º
El valor de un ángulo exterior de un triángulo es igual a la suma de los dos interiores no adyacentes.
α = B + C
3. Un ángulo interior y exterior de un triángulo son suplementarios, es decir, suman 180º.
α = 180º – A
Suma de ángulos interiores y exteriores de un cuadrilátero
Un cuadrilátero es un polígono de cuatro lados, los ángulos interiores de un cuadrilátero suman 360°
Un cuadrado suma 360°, 90° + 90° + 90° + 90° = 360°
Suma de ángulos interiores y exteriores de un Pentágono
Un pentágono tiene 5 lados, y se puede dividir en tres triángulos, así que sus ángulos interiores suman 3 × 180° = 540°
Y si es regular (todos los ángulos son iguales), cada uno mide 540° / 5 = 108°
Regla general
Cada vez que añadimos un lado más (de triángulo a cuadrilátero, a pentágono, etcétera) sumamos otros 180°al total:
DIAGONALES
Las diagonales de un polígono son segmentos que unen dos vértices no consecutivos.
El número de diagonales (D) de un polígono convexo (sea o no regular) viene determinado por el número de lados (N) que tiene el polígono. Su fórmula es:
Esto es así porque de cada vértice sale una diagonal a los demás vértices, excepto a sí mismo y sus dos consecutivos (de ahí el -3). Como una diagonal la trazamos entre dos vértices dos veces, una en cada sentido, el resultado del numerador se tiene que dividir por 2.
Ejemplo:
Un cuadrado tiene 4 lados. Se aplica la fórmula para comprobar el número de diagonales
El cuadrado tiene dos diagonales. Si la longitud de los lados son conocidos, se puede calcular la longitud de las diagonales.
PERíMETROS Y ÁREAS:
Definición de área
El área de un polígono es la medida de la región o superficie encerrada por un polígono.
Perímetro del triangulotriángulo equilátero:
triángulo isósceles:
triángulo escaleno:
Ejercicio:
Hallar el área y el perímetro del siguiente triángulo:
P = 2 · 11 + 7.5 = 29.5 cm
Poliedros Elementos y clasificación
En un poliedro podemos distinguir los siguientes elementos:
Caras: son los polígonos que forman el poliedro.

Aristas: son los segmentos donde hacen intersección las caras.
Vértices: son los puntos donde hacen intersección las aristas.
Además podemos citar los ángulos diedrosdelimitados por dos caras que se cortan.
Ángulo diedro es la región del espacio delimitada por los semiplanos que contienen dos caras que se cortan.
Hay tantos como número de aristas.
También encontramos ángulos poliedros determinados por las caras que inciden en un mismo vértice.
Ángulo poliedro es la región del espacio delimitada por los semiplanos que contienen las caras que inciden en un vértice.
Hay tantos como número de vértices.
CLASIFICACIÓN:
Los poliedros se pueden nombrar y clasificar según distintos criterios. Se podrían hacer muchas consideraciones al respecto,
pero hemos pensado que lo mejor es simplificar la situación para poder entenderlo mejor:
- Clasificación según su NÚMERO DE CARAS. Para ello, se cuenta el número totales de caras de un poliedro, y
se construye su nombre utilizando términos provenientes del griego clásico: tetraedro, pentaedro, hexaedro, heptaedro… (La primera parte indica el número de caras y la partícula “edro” significa “cara”).
Si te fijas, es la misma forma que se utiliza para nombrar a los polígonos según su número de lados.
- Clasificación según su REGULARIDAD. Se clasifican en poliedros regulares e irregulares. Para que un polígono
sea regular, debe tener todas sus caras, aristas y ángulos iguales. Lo que pasa es que solo existen 5 poliedros que tengan estas
características. También se les llama SÓLIDOS PLATÓNICOS.
- Clasificación en convexos y cóncavos. Se considera que un
poliedro es convexo si dos puntos cualesquiera del poliedro se pueden unir
con una línea que no salga del poliedro.
La mayoría de poliedros cóncavos tienen algún ángulo mayor de 180°
.
Muchos poliedros cóncavos se consideran “poliedros estrellados”.
A continuación mostramos un deltaedro convexo y otro deltaedro cóncavo.
- Clasificación según sus CARAS. Según esto podemos distinguir varias situaciones:
· Poliedro de caras regulares: todas sus caras son polígonos regulares (aunque pueden ser polígonos distintos, y ser
Distintas sus aristas). Aquí se incluyen los 5 sólidos platónicos y otros muchos poliedros.
· Poliedros de caras uniformes: todas sus caras son iguales (aunque pueden ser polígonos irregulares, o ser su aristas
Distintas. Aquí se incluyen los 5 sólidos platónicos y otros muchos poliedros.
- Clasificación según sus aristas: Se denominan poliedros de aristas uniformes a aquellos en los que una arista
Contiene un par de caras, que son iguales a otro par de caras de cualquier otra arista.
- Clasificación según sus de vértices: se denominan poliedros de vértices uniformes a aquellos en los que en un
Vértice convergen el mismo número de caras y en el mismo orden.
- Clasificación según sus CARACTERÍSTICAS (familias de poliedros). Es la forma más usual y actual de
Clasificar y nombrar a los poliedros. Se distinguen 2 grandes familias:
· Poliedros regulares o SÓLIDOS PLATÓNICOS: como antes hemos nombrado, deben tener todas sus caras, aristas y
Ángulos iguales. Solo existen 5: tetraedro, hexaedro o cubo, octaedro, dodecaedro e icosaedro, regulares.
· Poliedros no regulares: no tienen todas sus caras, aristas o ángulos iguales. Hay infinitos poliedros irregulares, por lo
Que, este gran grupo, se divide en familias, con numerosos poliedros (infinitos en muchos casos).
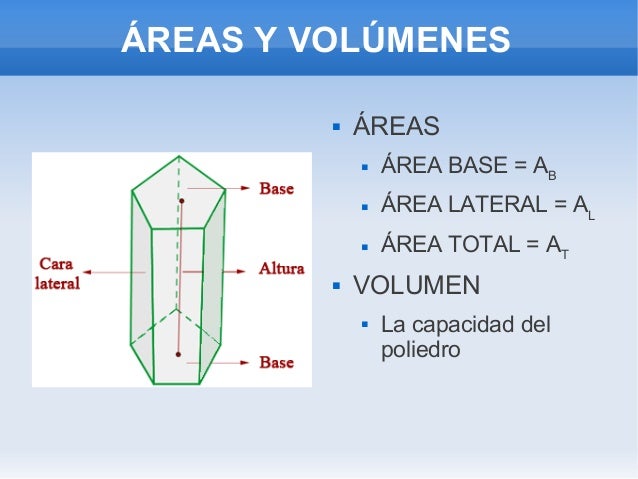
VOLÚMENES :
El volumen de un cubo se obtiene multiplicando el área de la base, por su altura.Como las caras que limitan al cubo son cuadrados,entonces el área de las bases corresponden al área del cuadrado que se obtiene multiplicando lado por lado.si se denota el área del cuadrado por A al lado por a; entonces A=a y como la altura del cubo también mide a, entonces el volumen V del cubo es igual al cubo o tercer potencia del lado.
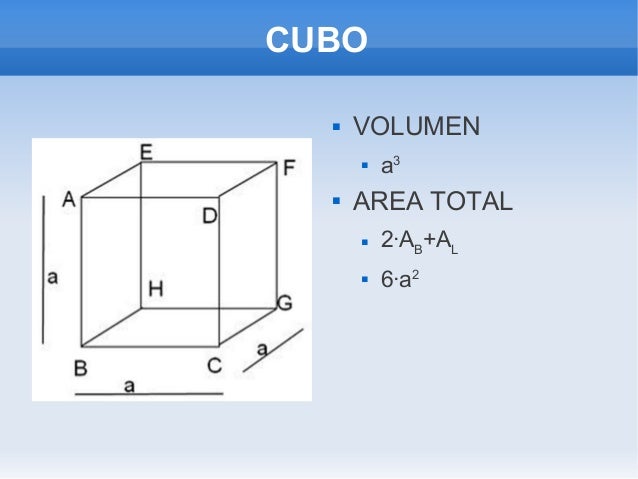
Ejercicio:
V=Bh
V=(42)(10)
=(16)(10)
=160cm ala tercera potencia

























No hay comentarios.:
Publicar un comentario