Elementos de la circunferencia

En la imagen expuesta arriba se pueden ver todos los elementos que vamos a nombrar a continuación:
Centro: punto central que está a la misma distancia de todos los puntos pertenecientes a la circunferencia.
Radio: pedazo de recta que une el centro con cualquier punto perteneciente a la circunferencia.
Cuerda: pedazo de recta que une dos puntos cualquiera de una circunferencia.
Diámetro: mayor cuerda que une dos puntos de una circunferencia. Hay infinitos diámetros y todos pasan por el centro de la circunferencia.
Recta secante: recta que corta dos puntos cualesquiera de una circunferencia.
Recta tangente: recta que toca a la circunferencia en un solo punto y es perpendicular a un radio.
Centro: punto central que está a la misma distancia de todos los puntos pertenecientes a la circunferencia.
Radio: pedazo de recta que une el centro con cualquier punto perteneciente a la circunferencia.
Cuerda: pedazo de recta que une dos puntos cualquiera de una circunferencia.
Diámetro: mayor cuerda que une dos puntos de una circunferencia. Hay infinitos diámetros y todos pasan por el centro de la circunferencia.
Recta secante: recta que corta dos puntos cualesquiera de una circunferencia.
Recta tangente: recta que toca a la circunferencia en un solo punto y es perpendicular a un radio.
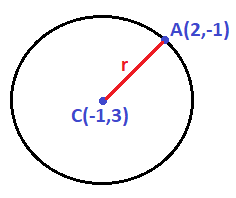
Ejercicio:Hallar la ecuación de la circunferencia que pasa por el punto A(2,-1) y cuyo centro es C(-1,3).
En este ejercicio conocemos el centro y un punto de la circunferencia:
Nos falta conocer el radio de la circunferencia para poder calcular su ecuación, que es igual a la distancia entre el punto A y el centro C:

Ahora ya conocemos el centro y el radio:
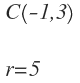
Por tanto, ya podemos calcular la ecuación de la circunferencia.
En la siguiente expresión:
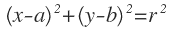
Sustituimos a, b y r por sus valores:
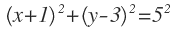
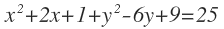
Y reordenamos términos para dejar la ecuación en su forma general:
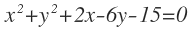
Video:
Circunferencia y círculo CONCEPTO DE CÍRCULO Y CINRCUNFERENCIA
Circunferencia y círculo CONCEPTO DE CÍRCULO Y CINRCUNFERENCIA
Circulo:
Un círculo es una superficie plana limitada por una línea curva (circunferencia).
A menudo se utiliza indistintamente círculo y circunferencia para nombrar la misma cosa, pero esto no es correcto. Circunferencia es una curva geométrica plana, cerrada, cuyos puntos son equidistantes (están a la misma distancia) del centro, y sólo posee longitud de la circunferencia, es decir, el perímetro del círculo.
Cabe destacar que aunque ambos conceptos están relacionados, no debe confundirse: la circunferencia es la línea curva y el círculo la superficie de la figura.
El círculo, al ser una figura plana (todos sus puntos están contenidos en un solo plano) tiene dos dimensiones y por lo tanto tiene área.

Circunferencia:
La circunferencia es una línea curva, cerrada y plana, cuyos puntos están todos a la misma distancia de otro punto, llamado centro.
Dimensión de la circunferencia: al ser una línea, la circunferencia tiene una sola dimensión, la longitud.
Centro de la circunferencia: punto del que equidistan todos los puntos de la circunferencia.
Centro de la circunferencia: punto del que equidistan todos los puntos de la circunferencia.
Radio de la circunferencia: segmento que une el centro de la circunferencia con cualquier punto de la misma.
Cuerda de la circunferencia: segmento que une dos puntos de la circunferencia, el radio es perpendicular a la cuerda en su punto medio.
Diámetro de la circunferencia: es una cuerda que pasa por el centro. Es la cuerda que mayor tamaño tiene.
Arco de la circunferencia: es la porción de circunferencia limitada por dos puntos de la misma, también se puede decir que es cada una de las partes en que una cuerda divide a la circunferencia

Para poder hablar de rectas y segmentos en la circunferencia primero se maneja el concepto de circunferencia que es el conjunto de todos los puntos de un plano que equidistan de otro punto llamado centro.
Las rectas y segmentos de la circunferencia son: radio, diámetro, cuerda, tangente, secante y arco mismos que se apreciarán y distinguirán con el apoyo de GEOGEBRA y para esto se debe dar clic en la liga RECTAS Y SEGMENTOS EN LA CIRCUNFERENCIA que se encuentra en la parte inferior de la siguiente imagen .
Las rectas y segmentos de la circunferencia son: radio, diámetro, cuerda, tangente, secante y arco mismos que se apreciarán y distinguirán con el apoyo de GEOGEBRA y para esto se debe dar clic en la liga RECTAS Y SEGMENTOS EN LA CIRCUNFERENCIA que se encuentra en la parte inferior de la siguiente imagen .
Al trabajar las rectas y segmentos en la circunferencia hay que tener presente los siguientes teoremas:
- El diámetro divide a la circunferencia y al círculo en dos partes iguales.
- El diámetro es la mayor cuerda de la circunferencia.
- · En una circunferencia, o en circunferencias iguales, a cuerdas iguales corresponden arcos iguales, y si dos cuerdas son desiguales, a la mayor corresponde mayor arco.
- · La tangente a una circunferencia es perpendicular al radio en el punto de contacto
Ejercicio:Un ejemplo de circunferencia lo podemos encontrar en...
ANGULOS EN LA CIRCUNFERENCIA
Ángulo central es el ángulo que tiene su vértice en el centro de la circunferencia y los lados son radios de ella.

La medida del arco AB es la del ángulo central AOB.
Arco AB = Angulo AOB
Arco AB = Ángulo AOB
Esta igualdad nos permite medir en función del ángulo central o arco el resto de ángulos que pueden definirse en la circunferencia.
Angulo inscrito es aquel que tiene su vértice en la circunferencia.
El ángulo semiinscrito, (uno de los segmentos secante y el otro tangente) es un caso particular, o caso límite.
El ángulo inscrito mide la mitad que el arco que comprende.
Angulo interior, tiene su centro en un punto interior del círculo.
La medida del ángulo interior es la semisuma de los arcos que comprenden él y su opuesto.
Ángulo exterior es aquel que tiene su vértice en un punto exterior de la circunferencia, pudiendo ser sus lados, tangentes o secantes a la misma.
La medida del ángulo exterior es la semidiferencia de los arcos que abarca.
Ejercicios:

Perímetro de la circunferencia
Dada una circunferencia, el perímetro de una circunferencia es la longitud de la curva,
es decir, la distancia que caminaría una persona que empezara a caminar en un punto
de la circunferencia y diera una vuelta alrededor de la circunferencia hasta llegar al punto
de partida.
es decir, la distancia que caminaría una persona que empezara a caminar en un punto
de la circunferencia y diera una vuelta alrededor de la circunferencia hasta llegar al punto
de partida.
De igual manera que para el área, existe una expresión que nos permite saber la longitud
(o perímetro) de la circunferencia sólo conociendo su radio "r"
(o perímetro) de la circunferencia sólo conociendo su radio "r"
La expresión es la siguiente:
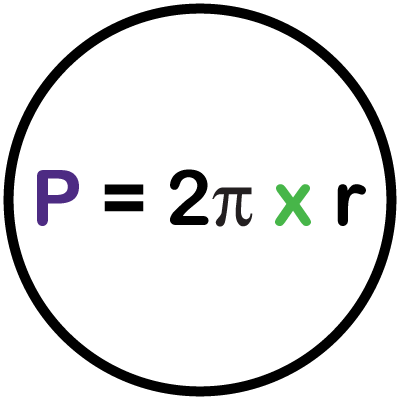
Ejercicio:
Calcula el área de un círculo cuyo radio es igual a 20 cm.
Tenemos como dato que el r=20 cm.
Por tanto, a partir de la fórmula del área del círculo:

Sustituimos r por 20 y operamos:

El área del círculo es de 1256,63 cm²
AREA DEL CÍRCULO
El área del círculo es igual al producto de π por el radio (r) al cuadrado.
También se puede calcular el área conociendo el diámetro del círculo (D),
ya que éste es el doble del radio.
Como un círculo es un polígono regular de infinitos lados, podemos
aplicar la fórmula general del área del polígono regular:
aplicar la fórmula general del área del polígono regular:
Ejemplo:
Sea un círculo de radio conocido, siendo éste r=2 cm.
Aplicamos la fórmula anterior:
Y se obtiene que el área de un círculo de radio 2 cm es de 12,57 cm2.
Secciones de un círculo :
Sector circular
Considere la posibilidad de un círculo y dos puntos A y B pertenecen a ella.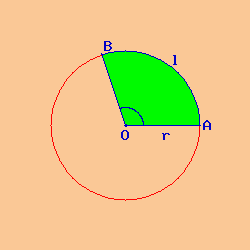
Nos sumamos con un punto de un segmento con el centro O del círculo y el punto B siempre con el centro O; considerar la parte del círculo entre el arco AB y el ángulo en el centro de AÔB; Esta parte se denomina sector circular ya que es una parte del círculo. La extensión del sector circular de la superficie de la zona llamada del sector circular y denota por As.
Entre el sector de la zona y el ángulo en el centro hay una proporcionalidad directa, en el sentido de que cuanto mayor es el ángulo en el centro mayor es el área del sector circular; De hecho, el sector es una parte de un círculo. Cuando el ángulo central es 360° sector de la zona que es igual al área del círculo.
Ejemplo
El área de un círculo es 100 π cm2; Calcular el área del sector circular subtendido por AB sabiendo que el ángulo AÔB al centro es de 90°.
ProgresoAplico la fórmula:

Recordando que el área del círculo es:
A = r·r· 3,14 = 100 π cm2
Pongo los valores y me sale:

Respuesta
El área del sector circular es de 25π cm2.
Corona circular:
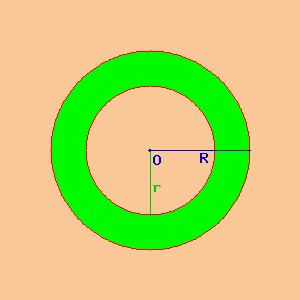
Dibujamos dos círculos de un radio r y un radio R, más grandes que r. La corona circular es la parte de la superficie entre los dos circunferencia.
Para calcular el área de la corona sólo hacer la diferencia entre el área del círculo exterior de radio R y el área del círculo interior de radio r.
Ejemplo:
A cuernos circulares interiores tiene un radio r = 20 cm y exteriores radio R = 30 cm. Calcular el área de la corona circular.
Progreso
En primer lugar el cálculo del área del círculo exterior con la fórmula:
Ae = R x R x 3,14159
y me sale:
Ae = 30 cm x 30 cm x 3,14159 = 2827,431 cm²
Cálculo y, a continuación, el área del círculo interior con la fórmula:
Ai = r x r x 3,14159
y me sale:
Ai = 20 cm x 20 cm x 3,14159 = 1256,636 cm²
Hago la diferencia entre el área del círculo exterior y el área del círculo interior.
por lo que:
Ac = Ae - Ai = 2827,431 - 1256,636 = 1570,795 cm² = 500 π cm²
Respuesta
El área de la corona circular es 1570.795 cm².
Trapecio circular:

Para calcular el área de la corona sólo hacer la diferencia entre el área del círculo exterior de radio R y el área del círculo interior de radio r.
Ejemplo:
A cuernos circulares interiores tiene un radio r = 20 cm y exteriores radio R = 30 cm. Calcular el área de la corona circular.
Progreso
En primer lugar el cálculo del área del círculo exterior con la fórmula:
Ae = R x R x 3,14159
y me sale:
Ae = 30 cm x 30 cm x 3,14159 = 2827,431 cm²
Cálculo y, a continuación, el área del círculo interior con la fórmula:
Ai = r x r x 3,14159
y me sale:
Ai = 20 cm x 20 cm x 3,14159 = 1256,636 cm²
Hago la diferencia entre el área del círculo exterior y el área del círculo interior.
por lo que:
Ac = Ae - Ai = 2827,431 - 1256,636 = 1570,795 cm² = 500 π cm²
Respuesta
El área de la corona circular es 1570.795 cm².
Trapecio circular:
Un trapecio circular es la parte de una corona circular comprendida entre dos radios del círculo mayor.
Área del trapecio circular
El área del trapecio circular es el resultado de restarle al sector circular mayor el sector circular menor.
También se puede calcular con el ángulo en radianes.

Ejercicio:
Hallar el área de un trapecio circular que pertenece a una corona circular de radios 5 y 3. Los radios que lo delimitan forman un ángulo de 60°.
Por lo tanto, tenemos que el radio mayor es R = 5 cm, el radio menor es r = 3 cm y el ángulo α = 60°.

Y se obtiene que el área de este trapecio circular es de 8,39 cm2.
ÁREA DE REGIONES SOMBREADAS
Una figura sombreada es una figura geométrica no convencional, y se produce por la superposición de dos o más figuras geométricas tradicionales.
Para calcular las áreas sombreadas hay que calcular el área de cada una de las figuras y restar una de la otra.
Para comprender bien, lo mejor es partir con ejemplos simples:
En la figura, tenemos que calcular el área de la parte sombreada. Vemos que esta se obtiene de la superposición de un círculo dentro de un cuadrado.
Entonces, tenemos que calcular el área del cuadrado y a esta restarle el área del círculo.
Ejemplo:
Calcular el área sombreada de la figura:
Vemos que sobre un cuadrado de 8 cm de lado se han superpuesto dos semicírculos cuyo diámetro es 8 cm.
Calculemos:
Área del cuadrado: A = L x L → 8 x 8 = 64 cm 2
En realidad, los dos semicírculos forman un círculo completo, por ello calculamos:
Como el diámetro del círculo es 8 cm, su radio será 4 cm.
Área del círculo: A = ∏r 2 → 3,1416 (4) 2 → 3,1416 (16) → 50,27 cm 2
Ahora, al área del cuadrado le restamos el área del círculo y tenemos
64 ̶ 50,27 = 13,73 cm 2 es el área sombreada.
|















No hay comentarios.:
Publicar un comentario